Aspects Algébriques
- 1.
- Montrer que si
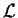 est un langage rationnel, alors
est un langage rationnel, alors
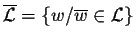 est rationnel.
est rationnel.
- 2.
- Montrer que le langage
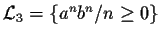 n'est pas
rationnel. En déduire que les langages
n'est pas
rationnel. En déduire que les langages
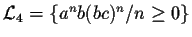 ;
;
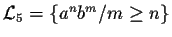 ;
;
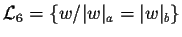 ne sont pas rationnels.
ne sont pas rationnels.
- 3.
- Soit
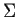 un alphabet contenant une seule lettre a. On
appellera suite arithmétique sur
un alphabet contenant une seule lettre a. On
appellera suite arithmétique sur 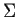 tout
langage de la forme :
tout
langage de la forme :
Montrer que
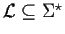 est rationnel
si et seulement si
est rationnel
si et seulement si 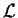 est une réunion finie de
langages d'ensembles finis ou de suites arithmétiques.
est une réunion finie de
langages d'ensembles finis ou de suites arithmétiques.
- 4.
- Soit
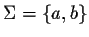 ,
,
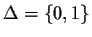 ,
,
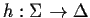 tel que h(a)=00, h(b)=010, et
tel que h(a)=00, h(b)=010, et
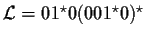 .
Montrer que
.
Montrer que
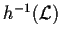 est reconnaissable; déduisez une expression rationnelle pour
est reconnaissable; déduisez une expression rationnelle pour
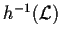 .
.
Jean-Baptiste Yunes
2000-02-18