Informatique Graphique
On se propose de calculer differentes projections d'un cube
sur un écran. Le cube 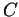 est centré en
est centré en 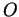 (origine de
l'espace), les coordonnées des 8 coins sont :
(origine de
l'espace), les coordonnées des 8 coins sont :
![$P_1= \left[{-100},{-100},{-100}\right] $](img3.png) ,
,
![$P_2= \left[{-100},{+100},{-100}\right] $](img4.png) ,
,
![$P_3= \left[{+100},{+100},{-100}\right] $](img5.png) ,
,
![$P_4= \left[{+100},{-100},{-100}\right] $](img6.png) ,
,
![$P_5= \left[{-100},{-100},{+100}\right] $](img7.png) ,
,
![$P_6= \left[{-100},{+100},{+100}\right] $](img8.png) ,
,
![$P_7= \left[{+100},{+100},{+100}\right] $](img9.png) ,
,
![$P_8= \left[{+100},{-100},{+100}\right] $](img10.png) . Pour chaque face :
. Pour chaque face :
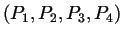
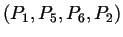
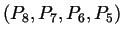
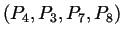
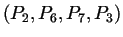
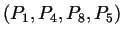 trouver la normale orientée vers l'extérieur.
L'écran de projection est un plan parallèle au plan
trouver la normale orientée vers l'extérieur.
L'écran de projection est un plan parallèle au plan 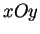 et
qui coupe la droite
et
qui coupe la droite 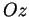 au point
au point
![$ \left[{0},{0},{-200}\right] $](img19.png) . L'
. L'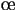 il
de l'observateur est situé au point
il
de l'observateur est situé au point
![$o= \left[{0},{0},{-300}\right] $](img21.png) .
Donner l'image de la projection du cube. Comment peut-t'on
éliminer les faces cachées (voir l'algorithme de Roberts) ?
.
Donner l'image de la projection du cube. Comment peut-t'on
éliminer les faces cachées (voir l'algorithme de Roberts) ?
Ensuite faire tourner le cube d'un angle de 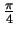 autour
de l'axe
autour
de l'axe 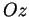 , puis d'un angle de
, puis d'un angle de 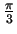 autour de l'axe
autour de l'axe
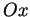 . Donner l'image de la projection du cube. Eliminer les
faces cachées.
. Donner l'image de la projection du cube. Eliminer les
faces cachées.
Jean-Baptiste Yunes
2002-01-21
![]() autour
de l'axe
autour
de l'axe ![]() , puis d'un angle de
, puis d'un angle de ![]() autour de l'axe
autour de l'axe
![]() . Donner l'image de la projection du cube. Eliminer les
faces cachées.
. Donner l'image de la projection du cube. Eliminer les
faces cachées.