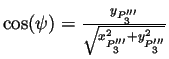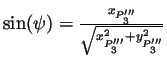InfoGraphie
Soit un trièdre
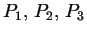 situé dans un repère
situé dans un repère 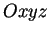 .
Le problème est de trouver la transformation permettant de
transporter
.
Le problème est de trouver la transformation permettant de
transporter 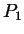 à l'origine, positionner
à l'origine, positionner 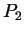 sur l'axe
sur l'axe 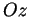 et
placer
et
placer 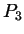 dans le plan
dans le plan 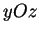 .
.
Pour réaliser cela il faut :
- faire une translation de
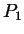 vers
vers 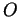 ,
,
- faire une rotation autour de
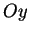 afin de placer
afin de placer 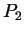 dans le
plan
dans le
plan 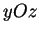 ,
,
- faire une rotation autour de
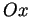 afin de placer
afin de placer 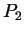 sur la
droite
sur la
droite 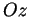 ,
,
- faire une rotation autour de
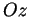 afin de placer
afin de placer 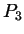 dans le
plan
dans le
plan 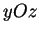 .
.
Soit les trois points :
![$ P_1=\mbox{$\left[
\begin{tabular}{c} $ x_1 $ $ y_1 $ $ z_1 $ $ 1 $ \end{tabular} \right]$} $](img11.png) ,
,
![$ P_2=\mbox{$\left[
\begin{tabular}{c} $ x_2 $ $ y_2 $ $ z_2 $ $ 1 $ \end{tabular} \right]$} $](img12.png) ,
,
![$ P_3=\mbox{$\left[
\begin{tabular}{c} $ x_3 $ $ y_3 $ $ z_3 $ $ 1 $ \end{tabular} \right]$} $](img13.png) .
.
La translation
![${\cal T}_{\stackrel{\rightarrow}{P_1O}}=
\mbox{$\left[
\begin{tabular}{cccc}
...
... & $ -z_1 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img14.png)
Donc on obtient la suite de points suivants :
![$ P'_1=\mbox{$\left[
\begin{tabular}{c} $ 0 $ $ 0 $ $ 0 $ $ 1 $ \end{tabular} \right]$} $](img15.png) ,
,
![$ P'_2=\mbox{$\left[
\begin{tabular}{c} $ x_2-x_1 $ $ y_2-y_1 $ $ z_2-z_1 $ $ 1 $ \end{tabular} \right]$} $](img16.png) ,
,
![$ P'_3=\mbox{$\left[
\begin{tabular}{c} $ x_3-x_1 $ $ y_3-y_1 $ $ z_3-z_1 $ $ 1 $ \end{tabular} \right]$} $](img17.png) .
.
On définit l'angle 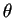 comme étant l'angle formé par la
projection de
comme étant l'angle formé par la
projection de 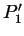 et
et 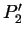 sur le plan
sur le plan 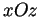 avec l'axe
avec l'axe 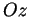 .
.
La rotation s'écrit
![${\cal R}_{Oy}(\theta)=
\mbox{$\left[
\begin{tabular}{cccc}
$ \cos(\theta) $...
...) $ & $ 0 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img22.png)
Or 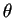 est un angle négatif (ie : c'est a dire qu'il
est dans le sens des aiguilles d'une montre lorsqu'on le suit
en étant placé sur la partie positive de l'axe de rotation et
que le regard porte vers l'origine). On a donc :
est un angle négatif (ie : c'est a dire qu'il
est dans le sens des aiguilles d'une montre lorsqu'on le suit
en étant placé sur la partie positive de l'axe de rotation et
que le regard porte vers l'origine). On a donc :
Donc la rotation s'écrit
![${\cal R}_{Oy}(\theta)=
\mbox{$\left[
\begin{tabular}{cccc}
$ \cos(-\theta) ...
...) $ & $ 0 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img25.png)
avec :
Donc on obtient la suite de points suivants :
![$P''_1=\mbox{$\left[
\begin{tabular}{c} $ 0 $ $ 0 $ $ 0 $ $ 1 $ \end{tabular} \right]$} $](img28.png) ,
,
![$P''_2=\mbox{$\left[
\begin{tabular}{c} $ 0 $ $ y_2-y_1 $ $ \frac{(x_2...
...1)^2}
{\sqrt{(x_2-x_1)^2+(z_2-z_1)^2}} $ $ 1 $ \end{tabular} \right]$} $](img29.png) ,
,
![$P''_3=\mbox{$\left[
\begin{tabular}{c} $ \frac{(x_3-x_1)(z_2-z_1)-(z_3-z_1)(x...
...z_1)}
{\sqrt{(x_2-x_1)^2+(z_2-z_1)^2}} $ $ 1 $ \end{tabular} \right]$} $](img30.png) .
.
On définit l'angle 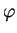 comme étant l'angle formé par
la droite
comme étant l'angle formé par
la droite
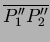 avec l'axe
avec l'axe 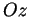 .
.
La rotation s'écrit
![${\cal R}_{Oz}(\varphi)=
\mbox{$\left[
\begin{tabular}{cccc}
$ 1 $ & $ 0 $ ...
...) $ & $ 0 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img33.png)
Cette fois l'angle 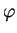 est mesuré positivement.
est mesuré positivement.
On définit l'angle 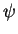 comme étant l'angle formé par la
projection de la droite
comme étant l'angle formé par la
projection de la droite
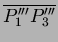 sur le plan
sur le plan 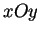 avec l'axe
avec l'axe 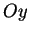 .
.
La rotation s'écrit
![${\cal R}_{0y}(\psi)=
\mbox{$\left[
\begin{tabular}{cccc}
$ \cos(\psi) $ & $...
...1 $ & $ 0 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img39.png)
Encore une fois on peut remarquer que l'angle est mesuré positivement.
Jean-Baptiste Yunes
2002-01-21
![$ P_1=\mbox{$\left[
\begin{tabular}{c} $ x_1 $ $ y_1 $ $ z_1 $ $ 1 $ \end{tabular} \right]$} $](img11.png) ,
,
![$ P_2=\mbox{$\left[
\begin{tabular}{c} $ x_2 $ $ y_2 $ $ z_2 $ $ 1 $ \end{tabular} \right]$} $](img12.png) ,
,
![$ P_3=\mbox{$\left[
\begin{tabular}{c} $ x_3 $ $ y_3 $ $ z_3 $ $ 1 $ \end{tabular} \right]$} $](img13.png) .
.
![${\cal T}_{\stackrel{\rightarrow}{P_1O}}=
\mbox{$\left[
\begin{tabular}{cccc}
...
... & $ -z_1 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img14.png)
![$ P'_1=\mbox{$\left[
\begin{tabular}{c} $ 0 $ $ 0 $ $ 0 $ $ 1 $ \end{tabular} \right]$} $](img15.png) ,
,
![$ P'_2=\mbox{$\left[
\begin{tabular}{c} $ x_2-x_1 $ $ y_2-y_1 $ $ z_2-z_1 $ $ 1 $ \end{tabular} \right]$} $](img16.png) ,
,
![$ P'_3=\mbox{$\left[
\begin{tabular}{c} $ x_3-x_1 $ $ y_3-y_1 $ $ z_3-z_1 $ $ 1 $ \end{tabular} \right]$} $](img17.png) .
.
![${\cal R}_{Oy}(\theta)=
\mbox{$\left[
\begin{tabular}{cccc}
$ \cos(\theta) $...
...) $ & $ 0 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img22.png)
![]() est un angle négatif (ie : c'est a dire qu'il
est dans le sens des aiguilles d'une montre lorsqu'on le suit
en étant placé sur la partie positive de l'axe de rotation et
que le regard porte vers l'origine). On a donc :
est un angle négatif (ie : c'est a dire qu'il
est dans le sens des aiguilles d'une montre lorsqu'on le suit
en étant placé sur la partie positive de l'axe de rotation et
que le regard porte vers l'origine). On a donc :
![${\cal R}_{Oy}(\theta)=
\mbox{$\left[
\begin{tabular}{cccc}
$ \cos(-\theta) ...
...) $ & $ 0 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img25.png)
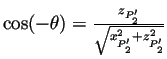
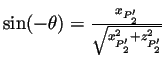
![$P''_1=\mbox{$\left[
\begin{tabular}{c} $ 0 $ $ 0 $ $ 0 $ $ 1 $ \end{tabular} \right]$} $](img28.png) ,
,
![$P''_2=\mbox{$\left[
\begin{tabular}{c} $ 0 $ $ y_2-y_1 $ $ \frac{(x_2...
...1)^2}
{\sqrt{(x_2-x_1)^2+(z_2-z_1)^2}} $ $ 1 $ \end{tabular} \right]$} $](img29.png) ,
,
![$P''_3=\mbox{$\left[
\begin{tabular}{c} $ \frac{(x_3-x_1)(z_2-z_1)-(z_3-z_1)(x...
...z_1)}
{\sqrt{(x_2-x_1)^2+(z_2-z_1)^2}} $ $ 1 $ \end{tabular} \right]$} $](img30.png) .
.
![${\cal R}_{Oz}(\varphi)=
\mbox{$\left[
\begin{tabular}{cccc}
$ 1 $ & $ 0 $ ...
...) $ & $ 0 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img33.png)
![]() est mesuré positivement.
est mesuré positivement.
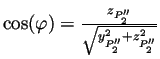
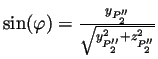
![${\cal R}_{0y}(\psi)=
\mbox{$\left[
\begin{tabular}{cccc}
$ \cos(\psi) $ & $...
...1 $ & $ 0 $ \\
$ 0 $ & $ 0 $ & $ 0 $ & $ 1 $ \\
\end{tabular}\right]$}$](img39.png)