Informatique Graphique
Le problème est de réaliser la rotation d'angle 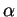 d'un
point
d'un
point 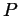 autour d'un point
autour d'un point 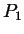 .
.
- Réaliser la rotation d'angle
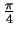 du point
du point
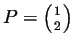 autour de
autour de
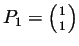 , quelles sont les
coordonnées du point
, quelles sont les
coordonnées du point 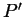 (image de
(image de 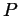 après la transformation) ?
après la transformation) ?
- Généraliser cette transformation pour un angle
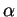 quelconque et des points
quelconque et des points 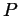 et
et 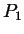 quelconques, et en tirer les
équations de la transformation ?
quelconques, et en tirer les
équations de la transformation ?
- Peut-on exprimer cette transformation sous forme d'une matrice ?
Utiliser le résultat précédent pour :
- Réaliser la transformation consistant à «faire tourner»
d'un angle de
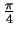 le carré formé des points
le carré formé des points
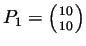 ,
,
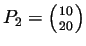 ,
,
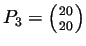 ,
,
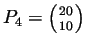 , autour du point
, autour du point 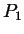 .
.
- Réaliser la rotation d'angle
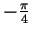 du carré obtenu
autour de
du carré obtenu
autour de 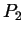 .
.
- À quoi correspond une telle transformation ?
- Peut-t'on commuter une rotation et un changement d'échelle ?
- Peut-t'on commuter une translation et un changement d'échelle ?
- Peut-t'on commuter une rotation et une translation ?
- Peut-t'on inverser un cisaillement ? Si oui, quelle est la
transformation inverse ? Si non, pourquoi ?
Jean-Baptiste Yunes
2002-01-21