Aspects Algébriques

Les mots

1.

(Lemme de Levi). Montrer que $\forall x,y,z,t\in {\tt A}^\star$ :

$$xy=zt\Rightarrow\exists u\in {\tt A}^\star,\left\{\begin{tabu... ... \\ ou \\ $xu=z \mbox{ et } y=ut$ \\ \end{tabular}\right.$$

2.

  Enumérer les mots de longueur inférieure à 3 sur ${\tt A}=\{a,b\}$.

3.

On définit sur ${\tt A}^\star$ les relations $\leq_l$ et $\leq_g$ par :

$$\begin{tabular}{rcl} $u\leq_l v$ & $\Leftrightarrow$ & $\lef... ...x{ et }u\leq_l v$ \\ \end{tabular}\right.$ \\ \end{tabular}$$

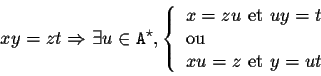
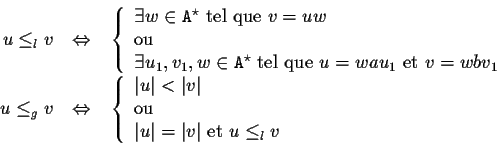
Ordonner les mots de l'exercice 2 selon $\leq_l$ et $\leq_g$, puis les mots de l'ensemble :

$$\{bab,1,ab,aab,bba,aaab,aa\}$$

4.

Montrer que $\leq_l$ et $\leq_g$ sont des ordres totaux sur ${\tt A}^\star$.

5.

Pour $\leq_l$ et $\leq_g$ dire si tout élément de ${\tt A}^\star$ possède un plus grand prédecesseur et un plus petit successeur.

6.

$\leq_l$ et $\leq_g$ sont-elles stables pour la concaténation à gauche et à droite ?

7.

La concaténation est-elle simplifiable à gauche et à droite ?

8.

Soit $w\in {\tt A}^\star,w=a_1a_2\ldots a_n$. L'image mirroir (ou le renversé) de w est le mot $\overline{w}=a_n\ldots a_2a_1$.

Un mot $w\in {\tt A}^\star$ est un palindrome si et seulement si $\vert w\vert\leq 1$ ou $\exists x\in {\tt A},w=xux$ avec u palindrome.

Montrer que w est un palindrome si et seulement si $w=\overline{w}$.

9.

Deux mots $u,v\in {\tt A}^\star$ sont dits conjugués s'il existe $f,g\in {\tt A}^\star$ tels que u=fg et v=gf.

(a)

Trouver tous les conjugués du mot abbaab.

(b)

Vérifier que la relation de conjuguaison est une relation d'équivalence.

10.

Soient $u,v,w\in {\tt A}^\star$. Donner une solution de l'équation uv=vw lorsque |u|=|w|=2 et |v|=5.

11.

Montrer que, de façon générale, on a :

$$uv=vw\Leftrightarrow(\exists f,g\in {\tt A}^\star\mbox{ et } p\leq0\mbox{ tel que }u=fg,w=gf,v=(fg)^pf=f(gf)^p)$$

12.

Montrer que uv=vu si et seulement si u et v sont puissance d'un même mot.