Aspects Algébriques
Rappel : Soit 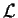 un langage. On définit la relation
suivante :
un langage. On définit la relation
suivante :
Rappel : Soit 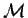 un automate. On définit la relation
suivante :
un automate. On définit la relation
suivante :
- 1.
- Soit
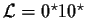 .
Combien ce langage
définit-il
de classes d'équivalences ? Donner une expression rationnelle
pour chacune d'elle.
.
Combien ce langage
définit-il
de classes d'équivalences ? Donner une expression rationnelle
pour chacune d'elle.
- 2.
- Montrer que si
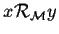 alors
alors
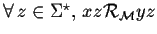 .
.
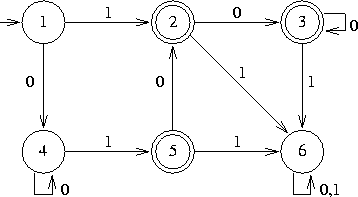
- 3.
- Donner les classes d'équivalences pour chacun des états de
l'automate
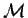 suivant :
suivant :
- 4.
- Montrer que la relation
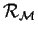 est plus fine que
la relation
est plus fine que
la relation
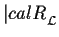 .
.
- 5.
- Montrer que
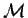 (du 3) reconnaît
(du 3) reconnaît 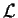 (du 1).
(du 1).
- 6.
- En déduire un automate ``minimal'' reconnaissant
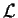 .
.
Jean-Baptiste Yunes
2000-02-18
![]() un automate. On définit la relation
suivante :
un automate. On définit la relation
suivante :